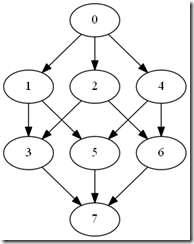
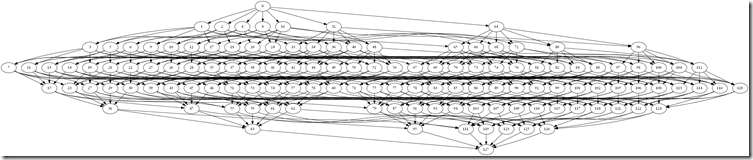
The Punch 22 Challenge is to find a 7-bit encoding of the 26 letters of the English alphabet that can be punched on a paper tape … twice. That is, after the tape has been used once with this encoding, it can be fed into a combination reader/writer machine that will punch additional holes to change to a different letter.

The first thing we notice about this encoding is that it has to have more than one hole pattern assigned to a letter. On the first write, with an unused tape, we write one pattern. On the second write, we choose a different pattern based on the holes that are already punched.

I’ll let you read the original article for a detailed description of the problem. What follows here is an analysis of the problem and then, if you scroll to the end, the solution. If you want to solve it yourself, stop reading now.

Tape costs more than people

Apparently, paper is really expensive. I am embarrassed to admit how much time I’ve spent on this problem, but I’m sure you could buy quite a lot of paper tape with my hourly rate for that duration. Nevertheless, once a problem is solved, the solution can be scaled. This may be an academic problem, but others like it have lead to some real advancements in our industry. Huffman Coding. Compression. Reliable magnetic storage.

At its heart, this is an Information Theory problem. How much information is in two punches of a tape? How can we compress all valid permutations of two characters down to 7 bits? How much of the information about the first character is retained after the second character is punched? And can you reconstruct with some probability the original message that was first written to the tape?

I love Information Theory, so this problem had me at the start.

Reachability

The problem is really one of reachability of nodes in a directed acyclic graph. When we punch a hole, we can go forward, but we can’t go back.

If you had 3 bits, they would form a graph that looks a little like a cube.

The graph of the full 7 bits looks a bit more complex.

But the concept is the same no matter how big or small the graph. Each of the numbers represents a symbol that we could punch on the tape. The arrows point to all the symbols that we can reach by punching one more hole. We can construct the set of all symbols reachable from a single starting point. These are all the symbols that I could punch over the starting symbol.

Suppose I had the symbol 42. This is the binary 0101010. It has three holes punched. From there, I could reach the following symbols:

This tells me that if there was a 42 on the tape, then I could only punch the 16 symbols that are reachable from that node. That’s key.

The initial symbols

Let’s review the problem. We need to create an encoding that allows the tape to be reused once. The encoding assigns a letter to each of the 128 possible symbols that I could punch. So what are the rules by which we will use this encoding?

When the machine needs to punch a letter, it first reads what’s already there. If this is the first time using the tape, then no holes are punched; it’s a zero. In that case, it will punch the initial symbol for the letter.

The second time through, each cell is going to contain one of the initial symbols. If I want to punch a different letter, then it has to be reachable from that initial symbol. If the current symbol already represents the letter, then you don’t need to change it. You have no idea what letter is coming next, so at least one symbol for every letter has to be reachable from each symbol in the initial set.

That means that 42 cannot be an initial symbol.

I can only reach 16 symbols from 42 (including 42 itself). By the pigeon-hole principle, I cannot assign 26 letters to 16 symbols.

Looking back at the graph, we can see that the symbol at the top – zero – can reach the entire graph. At the second tier, we have symbols with one hole punched. They can reach only those symbols that have that hole punched, which is half of them. The third tier has two holes punched. It cuts reachability in half again. 42 is in the fourth tier, with three holes punched, so it has cut the number in half three times. Each tier can reach half of what the prior tier could. Let’s label the tiers and count how many symbols are in each tier, and how much of the graph they can reach.

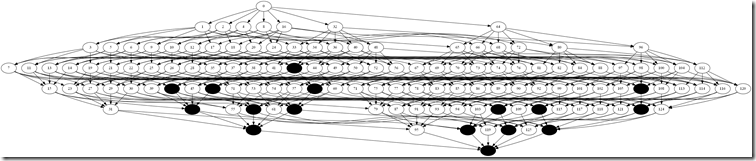
Since we need to assign distinct letters to the symbols reachable from every initial symbol, they must all be able to reach at least 26 symbols. All of the initial symbols must be in one of the first three tiers: P₀, P₁, or P₂. Lower tiers cannot reach enough symbols.

And since we have to assign 26 initial symbols, we have to consume the first three tiers with only 3 slots left. There are a total of 29 symbols available for us to choose. That means that at least 18 of the initial symbols are in P₂.

Parceling the alphabet

Now the challenge becomes assigning letters to the remaining tiers to be sure that the alphabet is covered from every symbol in P₂. The initial symbol at P₂ can reach itself, but the remaining 25 letters need to be accounted for in the lower tiers.

If we were to solve the problem for P₂, then P₀ and P₁ would be solved as well. P₀ has only one symbol – zero, and it can already reach the entire graph. P₁ has 7 symbols. Each one can reach 6 symbols in P₂ by punching one of the remaining holes. If any one these 6 symbols can reach the entire alphabet, then so can the initial symbol in P₁.

Remember that we have at least 18 initial symbols in P₂. How do we reach the alphabet from each of those 18 initial symbols? We can flip the problem, and instead ask how we can parcel out the 26 letters so that at least one symbol for each letter is reachable from all 18 of the initial symbols in P₂.

Let’s identify 26 sets of symbols that can be reached from at least 18 P₂s. The first set is easy. It contains only the symbol 127, or binary 1111111. The entire graph can reach this symbol. Unfortunately, there is only of those, and we still have 25 letters to assign.

Then we can construct a set based on the P₆s. These are the symbols with 6 ones, such as 126, or binary 1111110. The initial symbols with a one in the final position cannot reach this symbol, so we have to add symbols that they can reach. Each of these P2s has one other bit set, so we need to choose symbols that cover all possible pairs of bits. Let’s draw those symbols from the other sets. Here’s an example:

P₆: 1111110

P₄: 0001111

P₄: 1110001

This set consumes one P₆ and two P₄s. We only have 7 P₆s and 35 P₄s to go around, so if we define 7 such sets, we’ve spent all of our P₆s and 14 of our P₄s.

Let’s see if we can find a set that is less expensive. Again starting with a P₆ and a P₄, we can subdivide the remaining bits like this.

P₆: 1111110

P₄: 0001111

P₃: 0110001

P₂: 1000001

This takes more symbols, but we’ve spread the cost out a bit more. We can still only have 7 of these, since the P₆s are the limiting factor, but they leave a lot more of the P₄s for other sets to use. This set uses a P₂, which will be the initial symbol for the letter to which it is assigned.

I’ll let you go through the exercise of identifying the sets that can be reached from the P₂s. As you do, you can break them down by their cost in terms of symbols from each tier. This is what you will find:

The set S₆ is interesting. It consumes 2 P₂s. One of those P₂s will be the initial symbol for the letter to which it is assigned. The second will be one of the 3 remaining P₂s that are not initial symbols. So there can only be at most 3 letters in S₆.

The solution

Update: The following is incorrect. Stefan Stenzel (@5tenzel) showed me a solution to this problem, which let me reverse-engineer my mistake. See if you can spot it. Select the hidden text at the bottom of the post to reveal the solution.

And now we have enough information to solve the problem. All we need to do is determine how many of each set we can assign to the 26 letters of our alphabet. We can compute the cost in terms of symbols in each of the tiers P₂ through P₇. We know exactly how many of those symbols we have. So this is just an optimization problem.

The optimal way to assign those sets is:

1S₁, 7S₃, 10S₄, 4S₅, and 3S₆.

This consumes 1P₇, 7P₆, 17P₅, 34P₄, 35P₃, and 13P₂. We have no more P₃s left. We could trade an S₅ for an S₄ to get two more P₃s, but then we have no more P₄s left.

But this is only 25 sets. 1 + 7 + 10 + 4 + 3 = 25. We don’t have enough sets to assign to all 26 letters. The pigeon-hole principle strikes again.

So the solution is a non-solution. This is an impossible problem. Proving that it was impossible was difficult in itself. But it has provided us some value. For example, we know that we are likely to find a solution with a 25 letter alphabet. And we are likely to find a solution with an 8 hole tape. We won’t waste any time searching for a solution where we know that none can exist.

This type of proof – that a solution does not exist – has been extremely important in the history of computer science. I refer you to the Gödel Incompleteness Theorem, Church and Turing on the Entscheidungsproblem, Turing’s Halting Problem, and P vs NP.

The mistake

The mistake was that the P₂s that are not initial symbols are not consumed by a set. I made this mistake twice. First, I claimed that the P2 in a set must be the initial symbol of the assigned letter. That was wrong: it could be a leftover P₂. Second, I claimed that there could be no more that 3 sets containing 2 P₂s. That is incorrect because the leftover P₂s can appear in any number of sets.

To make matters worse, I did not create a complete table of sets. I gave up on combinations that I assumed would consume too many symbols. Complete the table and allow the leftovers to be reused, and you get plenty of wiggle room to allow a solution. Stefan’s solution had the following sets:

Which very neatly consumes 1P₇, 7P₆, 21P₅, 35P₄, and 30P₃. The P₂s are not all consumed, because many of them are the leftovers, reused from one set to the next.

Sefan’s solution is: ABCIDKMEEOQBSYTLFUWTYBGCTPDQNVWJGZ-YXGLZRJUVNDRPNWJXCFVKRZOMEISHH--SVTIUPDKRHSGNLYIWOMLRJKFECOZXJRZBJEYOXTICKWQFHSUNTQPDVLYGMUBA