|
|
Michael L Perry's blogConditionalsSubmitted by Michael L Perry on Fri, 07/16/2010 - 17:18
There is a bug in the following code. Fix the bug and prove that it is correct. public decimal GrowthPercent(decimal ThisQuarterSales, decimal LastQuarterSales) { if (LastQuarterSales == 0.0m && ThisQuarterSales == 0.0m) { // No sales means no growth. return 0.0m; } if (LastQuarterSales == 0.0m && ThisQuarterSales > 0.0m) { // Any sales over zero is interpreted as 100% growth. return 100.0m; } return (ThisQuarterSales / LastQuarterSales - 1.0m) * 100.0m; } View the solution. Conditionals solutionSubmitted by Michael L Perry on Fri, 07/16/2010 - 17:18
The code as written could divide by zero. It may look like division by zero has been prevented, but there is a code path that fails. here it is again. public decimal GrowthPercent(decimal ThisQuarterSales, decimal LastQuarterSales) { if (LastQuarterSales == 0.0m && ThisQuarterSales == 0.0m) { // No sales means no growth. return 0.0m; } if (LastQuarterSales == 0.0m && ThisQuarterSales > 0.0m) { // Any sales over zero is interpreted as 100% growth. return 100.0m; } return (ThisQuarterSales / LastQuarterSales - 1.0m) * 100.0m; } If ThisQuarterSales is negative, the code falls through to the division. We want to prove that LastQuarterSales is not zero before we divide by it. We can do this using conditionals. if (a) Assert(a); else Assert(!a); Think of the above code not as an algorithm that takes a single code path based on the value of “a”. Think of it as a logical statement. If A, then A. Otherwise, not A. It is obvious. And it can be applied to make the code obvious. if (LastQuarterSales == 0.0m) { Assert(LastQuarterSales == 0.0m); // ... } else { Assert(LastQuarterSales != 0.0m); return (ThisQuarterSales / LastQuarterSales - 1.0m) * 100.0m; } With this form, we can assert that LastQuarterSales is not zero before we divide by it. The code will never throw. Q.E.D. Let’s apply that form to the buggy code. public decimal GrowthPercent(decimal ThisQuarterSales, decimal LastQuarterSales) { if (LastQuarterSales == 0.0m) { Assert(LastQuarterSales == 0.0m); if (ThisQuarterSales == 0.0m) { // No sales means no growth. return 0.0m; } if (ThisQuarterSales > 0.0m) { // Any sales over zero is interpreted as 100% growth. return 100.0m; } } else { Assert(LastQuarterSales != 0.0m); return (ThisQuarterSales / LastQuarterSales - 1.0m) * 100.0m; } } The compiler will give you an error message. Not all code paths return a value. We can use the compiler’s inference engine to help us prove the correctness of our code. Change the conditions to ensure that all code paths return. public decimal GrowthPercent(decimal ThisQuarterSales, decimal LastQuarterSales) { if (LastQuarterSales == 0.0m) { Assert(LastQuarterSales == 0.0m); if (ThisQuarterSales <= 0.0m) { // No sales means no growth. return 0.0m; } else { // Any sales over zero is interpreted as 100% growth. return 100.0m; } } else { Assert(LastQuarterSales != 0.0m); return (ThisQuarterSales / LastQuarterSales - 1.0m) * 100.0m; } } By putting the division inside of an else, we’ve proven that it will not divide by zero. At that point, the compiler was able to help us find the code path that would otherwise have caused the bug. We fixed the bug, and the compiler helped us prove that it was fixed. The CAP Theorem and its ImplicationsSubmitted by Michael L Perry on Mon, 07/05/2010 - 18:17
Please access the materials on line: The CAP Theorem tells us that we have a choice. With our customer’s help, we choose the architecture that bets fits the system we are building. Some architectures guarantee Consistency and Availability. Others relax Consistency in favor of Partition Tolerance. Still others choose some guarantees for some subsystems and other guarantees for others. In this talk, I present the definition and proof of the CAP Theorem. I then describe the different types of systems that benefit from different guarantees. Finally, I present three different architectures and demonstrate in code how they each uphold their own guarantees. The slides are presented in Silverlight. This gives the presenter the ability to take notes in the sidebar, to pan and zoom through the diagrams, and to step through animations.
The code is written in C# 4.0, and can be opened in Visual Studio 2010. Its 9 projects are grouped into 3 examples:
Activate the Task List view to follow the TODO comments through the code. Always look at the entity model before walking through source code. To run the examples, you must first run the databases.sql script to create three databases:
Both the slides and the source code are licensed for your use under the Creative Commons Attribution 3.0 United States License. You are free to use either or both in any way you choose, including presenting the material yourself. Please retain the attribution in the title page. The CAP TheoremSubmitted by Michael L Perry on Mon, 06/21/2010 - 13:52
Eric Brewer is an expert in distributed systems. In the Principles of Distributed Computing 2000 keynote address, he gave us the CAP Theorem. It states that a distributed system cannot simultaneously guarantee these three attributes:
Consistency There are many ways to guarantee consistency. One would be to block writes until all nodes have been notified. Another would be to block reads until all nodes are consulted. Yet another is to delegate one node the master of that particular piece of data, and route all messages to it. In practice, consistent distributed systems use a combination of these algorithms. Availability You can see the tension between consistency and availability. To guarantee both, we need redundancy. What if the data that we try to read was only stored on the node that was lost after the write? That data would not be available, and we could not guarantee consistency. Partition Tolerance
Most distributed systems respond to momentary message loss by resending messages. But since the network cannot guarantee message delivery, even those retries might be lost. It’s how the system responds to maintained message loss that determines whether it can guarantee partition tolerance. Proof Or you can ask how a system can guarantee both consistency and availability. Remember our three example algorithms. If we block writes until every available node is notified, and those notifications are lost, then we must fail the write. If we block reads until every available node is consulted, and those messages are lost, we must fail the read. And if we delegate to the master, and that message is lost, then we fail as well. And finally, we can guarantee both availability and partition tolerance, but we have to relax our consistency guarantee. Nodes might be down and messages might be lost, but if we assume that those problems will eventually be solved, then we can say that we will eventually be consistent. It is possible to read stale data from such a system, but given enough time all nodes will be up-to-date. When designing a distributed system, consider the guarantees that the problem demands. But also consider the guarantees that you will be unable to make, and decide how best to respond in those situations. The case for IoC containersSubmitted by Michael L Perry on Wed, 01/20/2010 - 15:02
An IoC container helps make code more maintainable. It prevents changes to one part of a system from breaking other parts of the system. It allows developers to make those changes in isolation. And, in the case of the Q.E.D. IoC container, it encourages patterns that prove code correctness. The Dependency Inversion Principle (DIP) Let’s walk through an example that Uncle Bob often presents. A copy program reads from the keyboard and writes to the screen. static void Main() { Keyboard keyboard = new Keyboard(); Screen screen = new Screen(); while (true) { char c = keyboard.Read(); screen.Write(c); } } The Main method depends upon the Keyboard and Screen concrete classes. It cannot read from or write to anything else. This code is rigid. To make the code less rigid, we can invert the dependency. static void Main() { ICharacterSource keyboard = new Keyboard(); ICharacterTarget screen = new Screen(); Copy(keyboard, screen); } private static void Copy(ICharacterSource source, ICharacterTarget target) { while (true) { char c = source.Read(); target.Write(c); } } The Copy method depends upon abstract types (ICharacterSource and ICharacterTarget), not on concrete types. The Main method decides which concrete types to use. Now Copy is less rigid, because it can be called with anything that implements the right interface. Dependency injection Dependency injection is a way of achieving dependency inversion. It means that you pass dependent objects into a class. This can be done either through the constructor or through a property. Here’s an example of constructor injection: static void Main() { ICharacterSource keyboard = new Keyboard(); ICharacterTarget screen = new Screen(); Copier copier = new Copier(keyboard, screen); copier.Copy(); } class Copier { private ICharacterSource _source; private ICharacterTarget _target; public Copier(ICharacterSource source, ICharacterTarget target) { _source = source; _target = target; } public void Copy() { while (true) { char c = _source.Read(); _target.Write(c); } } } Q.E.D. prefers constructor injection over property injection because the constructor proves immutability. Inversion of control Inversion of control (IoC) containers facilitate dependency injection. Whereas manual dependency injection moves the concrete dependencies up the chain, an inversion of control container moves the dependencies outside of the source code entirely. If we were using an IoC container, the Main method would look like this: static void Main() { Copier copier = new Container().Resolve<Copier>(); copier.Copy(); } The IoC container would know that the Copier needs an ICharacterSource and an ICharacterTarget. Furthermore, it would know that Keyboard and Screen provide those services. It could therefore resolve that dependency with no additional information. Because dependencies are inverted, each class is less dependent upon other classes. We can change the behavior of one class simply by changing its dependencies. Because the IoC container is managing dependencies on our behalf, we can make changes in isolation. There is no need to change the caller when a class takes on a new dependency. And because we favor constructor injection, we can prove things like immutability. The Q.E.D. IoC containerSubmitted by Michael L Perry on Wed, 01/20/2010 - 15:01
Does the world need another inversion of control (IoC) container? No. But Q.E.D. does. Q.E.D. is a set of practices that make code more provable. It imposes constraints on the kinds of code we can write. When code is written within those constraints, it is easier to prove that it behaves correctly. Existing IoC containers do not impose these constraints. They allow property injection. They allow multiple constructors. They allow configuration. In order to prove the correctness of code, the Q.E.D. IoC container takes these features away. Dependent and independent object dataSubmitted by Michael L Perry on Thu, 01/07/2010 - 11:29
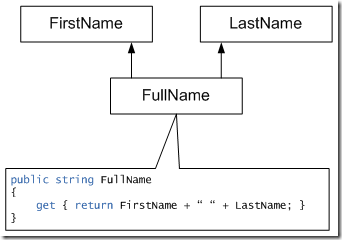
For example, a Person object has three properties: FirstName, LastName, and FullName. The user can directly set the first and last name, but the full name is derived. The user has no direct control over the full name. She can only influence it by changing the first or last name. Sometimes it's hard to see the difference between dependent and independent data. Both kinds of data change in response to a user action. The key question is not "when does it change", but rather "what determines its value". The UI might allow the user to enter a full name. When she types a new value, the UI parses the text she enters and determines the first and last names. It sets these two independent properties, and then calculates the full name. If the user entered well-formed input, the calculated output will be exactly the same. If not, the system will have "fixed" her mistakes (extra spaces, inconsistent formatting, etc.) The number of independent properties is exactly equal to the number of degrees of freedom that an object has. Ideally, independent properties are unconstrained. Constraints are codified in the dependent properties. Keep the data flowing Another strategy is to keep a marker for dependent data that is out-of-date. When the independent data changes, set the marker. When someone asks for the dependent data, check the marker. This postpones the update and therefore avoids redundancy. When dependent data in one object relies upon independent data in another, things get even more interesting. If you take the direct approach of notifying the dependent object from the independent one, you end up with tightly coupled objects. The observer pattern breaks that coupling. There are several other patterns that offer benefits over observer (including my own) that are too numerous to list here. Now add to the mix the fact that dependent data may rely on other dependent data. So a change to an independent property should result in the update of all of its direct and indirect dependencies. This could be accomplished through cascading notifications, whereby the direct dependent upon receipt of notice turns around and notifies the indirect dependent. But to avoid potential redundancy or cycles, this is more often handled through dependency analysis. That is certainly too deep for this post. Ebb and flow My synchronization framework starts with this fundamental concept. All object behavior is either dependent or independent. Degrees of freedomSubmitted by Michael L Perry on Wed, 01/06/2010 - 16:30
The equations slice through the volume. One equation with three unknowns makes a two-dimensional sheet that flaps in the volume. Two equations with three unknowns form a thread that curves through the system. The thread is not necessarily a straight line; it can swoop through in any of the three directions like a roller coaster. But if you were on the thread you could only walk forward or backward, so the thread is really one-dimensional. The number of unknowns minus the number of equations gives us the degrees of freedom. So that three-dimensional roller coaster with two equations has only one degree of freedom. If you were to start at the beginning and roll along the track, you could number each point as a distance from the start. That distance will have little to do with the straight-line proximity to the starting point, but since you can't leave the track it doesn't really matter. The equations that keep us on the track are constraints. If we have more equations than unknowns, the problem is over constrained. If we have fewer, the problem is under constrained and we have some degrees of freedom. If they are equal, then we have a Goldilocks problem: it's just right. We can usually find the one right answer to a Goldilocks problem. But software is not about finding one answer, it's about getting work done. And to get work done we need a little wiggle room. We need degrees of freedom. Find the degrees of freedom To identify the degrees of freedom in software, start by defining the unknowns. These are usually pretty simple to spot. These are the things that can change. In a checkbook program, for example, each transaction amount is an unknown, as are the the account balance and the color used to display it (black or red). Next, define the equations. These are the relationships between the unknowns that the software has to enforce. In the checkbook, the balance is the sum of all transaction amounts. And the color is red if the balance is negative or black otherwise. Subtract to find your degrees of freedom. One amount per transaction (n), one balance, and one color gives n+2 unknowns. The balance sum and the color rule give us two equations. n+2-2 = n degrees of freedom, one per transaction. Store the degrees of freedom Each degree of freedom represents something that the user can do. A user can enter transactions, but a user cannot directly edit the balance or the color. We need to store the user's direct inputs -- the degrees of freedom -- but not the related values. Those can be calculated when needed. Calculate the rest When the program needs a value that the user does not directly control, it should calculate it on the fly. The alternative is to store that value and adjust it whenever the user makes a relevant change. Sprinkle enough of these triggers through the system and it becomes a Rube Goldberg machine of cascading events. This is how software rots. Sometimes you want to store a calculated value for optimization. You might store an account balance if it needed to be read often, or if the number of transactions gets extremely large. But every time you make this kind of decision, you run the risk of inconsistency. Caches need to be invalidated, and changes accumulated. You might even choose to provide a "Refresh" button to spank the software and force it to reconcile. Be aware of every line of this extra code, as it is often the source of bugs. Understanding the degrees of freedom in the software helps to create a maintainable design. You know what is under the user's direct control, and what is affected indirectly. You know which values must be stored, and which must be calculated. And when you add new features in the future, you can add new degrees of freedom without affecting the previous ones. PredassertSubmitted by Michael L Perry on Mon, 01/04/2010 - 17:34
I was inspired by Robert C. Martin’s Clean Code to fix a problem with Microsoft’s unit testing framework. Assert.AreEqual(object expected, object actual). How do you remember which is the expected value and which is the actual? In JUnit and it’s younger .NET cousin NUnit, the method name makes it a bit more clear. Assert.assertEquals(Object expected, Object actual). The code reads more like a sentence (albeit one spoken by Yoda). assertEquals(3, theResult);I was further inspired by BDD systems like NSpec, which makes the code more grammatically correct. Specify.That( theResult ).ShouldEqual( 3 ); Readability of the code is only one of the concerns. The other is readability of the unit test failures. Assert.AreEqual() writes out a good failure message, because it can give you both the expected and the actual value. But more complex assertions do not provide useful failure messages. To solve these issues within the Microsoft unit testing space, I created Predassert. Yet another library with a class named “Is” The primary goal of Predassert is that one line of code expresses both a predicate and an assertion. A predicate is executable and can determine if something is true or false. An assertion is human readable and explains why a test fails. Predassert accomplishes this goal through a fluent interface. Pred.Assert( theResult, Is.EqualTo(3) ); The “Is” class declares several static methods that generate assertion predicates. For example: Pred.Assert( new List<Person>(), Is.Empty<Person>() ); Pred.Assert( referenceA, Is.SameAs(referenceB) ); Pred.Assert( bob, Is.NotNull<Person>() ); You also have “Has” for properties and “Contains” for collections. Pred.Assert( bob, Has<Person>.Property(person => person.Name, Is.EqualTo("Bob") ); Pred.Assert( queue, Contains<GameRequest>.That(Has<GameRequest>.Property( request => request.Person, Is.SameAs(bob)))); You can even combine predicates with “And”. Pred.Assert(bob, Has<Person>.Property(person => person.FirstName, Is.EqualTo("Bob") .And(Has<Person>.Property(person => person.LastName, Is.EqualTo("Perry")) ); As you can see, you can get pretty carried away. Uniformity of expression The fluent interface is not the goal. Uniformity of expression is the goal. The fluent interface is just a means to that end. When you use Microsoft’s unit testing framework, Assert.IsTrue(bool condition, string message) makes you express the assertion in both code and text. But when you use Predassert, the fluent interface generates both from the same syntax. The “Has” class will insert the property name into the assertion message. There is no need to retype it, no chance of copy/paste errors, and no extra work if you use the “Rename” refactoring tool. The “Contains” class will enumerate the collection and explain why each element failed the test. This extra detail usually gives you enough information to diagnose an error directly from the failure message, rather than by setting breakpoints. Predassert is currently distributed as part of the Correspondence library on CodePlex. I’m allowing it to grow organically as I need features. When it is more mature, perhaps I will separate it. Until then, you can download the Correspondence source code and extract the Predassert project for your own use. |